教育統計題庫及解答

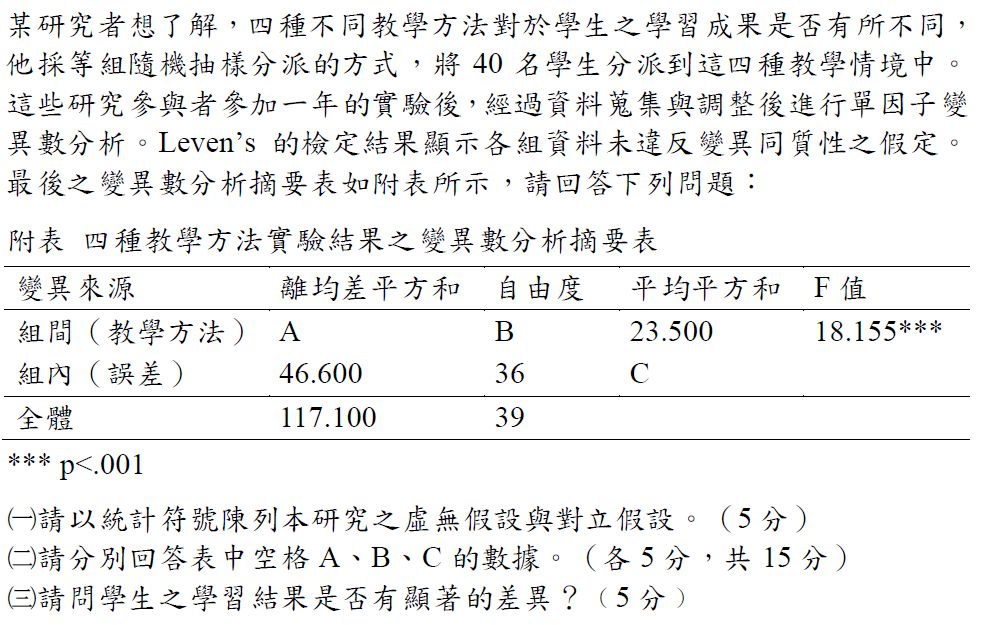
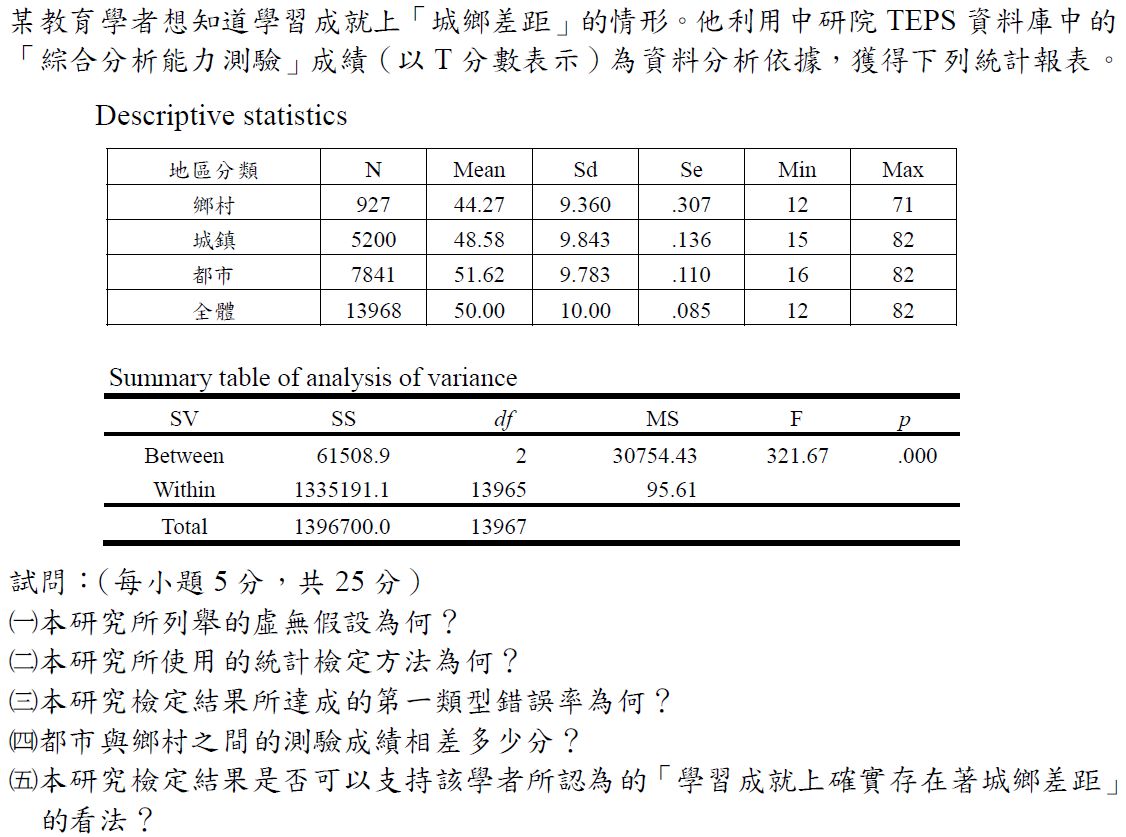
積差相關

109地特四等
請利用變異數的特性，回答下列問題：
(一)假設有N位受試者，每個人各有兩個測量變項( X 與 Y )的分數，已知其中的 X 變項的平均數為 10 分、變異數為 36 分，Y 變項的平均數為 12 分、變異數為 16 分，X項與變項之間的相關係數為.25。請問：若把每位受試者的這兩個變項分數先相加，使之成為一個合併變項分數，那麼，此合併變項分數的變異數是多少分?(8分)
(二)承上一題，若把每位受試者的這兩個變項分數先相減，使之成為一個合併變項分數，那麼，此合併變項分數的變異數是多少分?(8分)
(三)承上，如果把每位受試者的 X 變項都各加 4 分的話，則新的 X 變項的變異數是多少分?(5分)
(四)承上，如果把每位受試者的 Y 變項都各乘 4 分的話，則新的 Y 變項的變異數是多少分?(4分)

參考解答

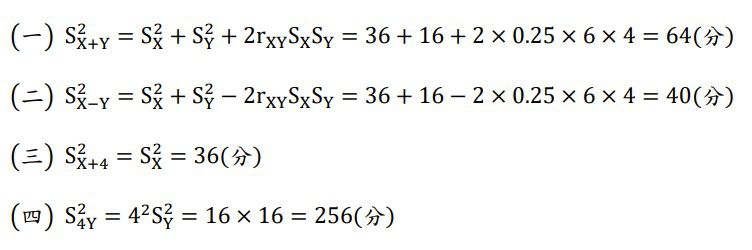
106原住民三等
請計算表二連續性資料X與Y兩變項的相關係數(25分)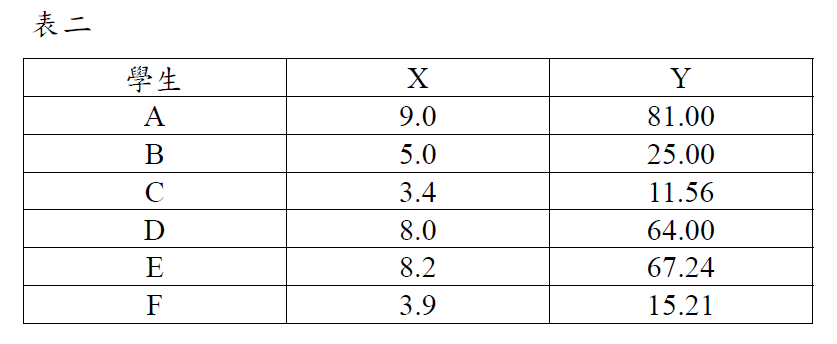

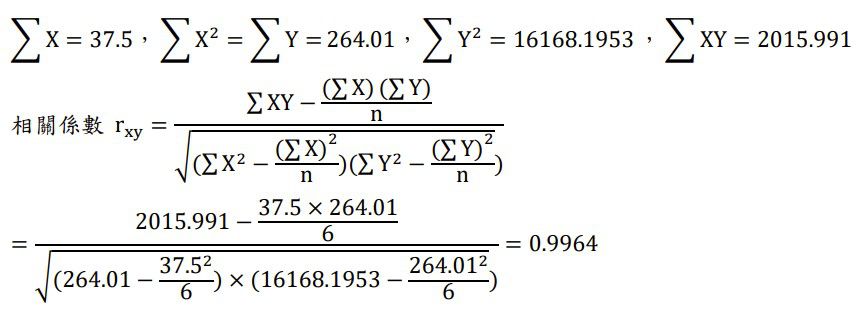
參考解答

104地特四等
(一)假設兩變項 X 與 Y 之相關數 r_xy=0.3，當兩變項都轉換成標準 z 分數後，兩變項之相關係數變成多少?(5分)
(二)當 r_xy= – 1.0且 Z_x=0.8時，Z_y 為多少?(5分)
(三)當 X 變項及 Y 變項的各個觀察值都乘上 4 倍後，其共變數的值又會變成原來共變數的多少倍?(5分)

參考解答

103身障四等
在計算積差相關係數或建立迴歸模型之前，通常先要繪製散佈圖(scatter plot)，何謂散佈圖?繪製散佈圖之目的為何?(10分)

參考解答

散佈圖：以X軸為自變項，Y軸為依變項，將變數資料放在直角坐標平面上。
繪製散佈圖的目的：用來判斷兩變數資料的相關關係和分佈狀況。從散佈圖中，我們可以觀察兩變數之間是否呈現線性關係還是非線性關係、線性關係的強弱和正負以及離群值的存在。

簡單迴歸分析

109普考
某統計學者收集到7名受試者樣本的智力分數(X)與學業成績分數(Y) ，其原始資料與標準化資料如下表所示：(每小題5分，共25分)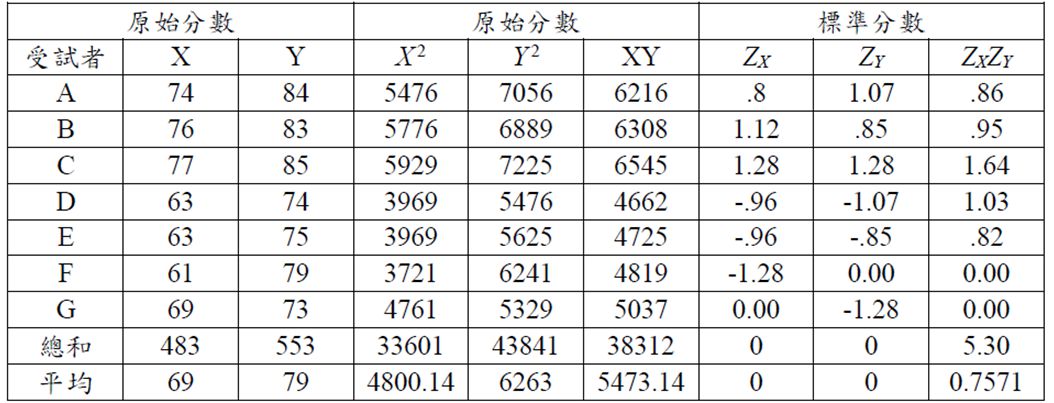

(一)X的變異數為何?
(二)X與Y的共變數為何?
(三)X與Y之間的相關係數是多少?
(四)X預測Y的標準化迴歸方程式為何?
(五)承上題，該迴歸方程式的決定係數為何?

參考解答

108司法三等(心理及教育統計)
研究者想探究學習動機是否能預測學習表現，3位學生的資料如下表所示，計算迴歸公式( Y=bX+a )?當 X=8 時，Y=?(25分)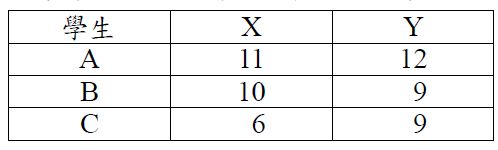

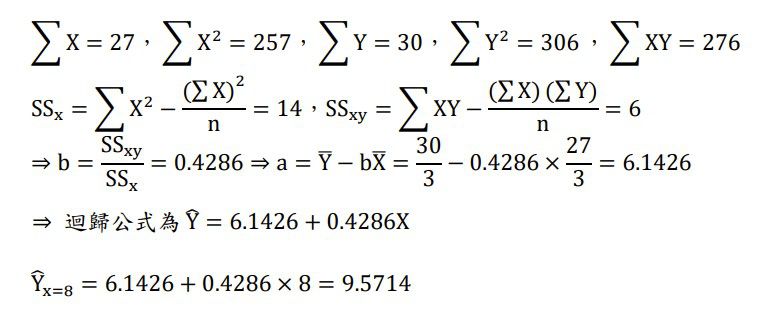
參考解答

102地特四等
下表為 8 位學生智商 (X) 與學業成績 (Y)：

(一)請計算 r_xy；a；b。(15分)
(二)若小華智商為 16 分，請預測他的學業成績會得幾分?(10分)

參考答案

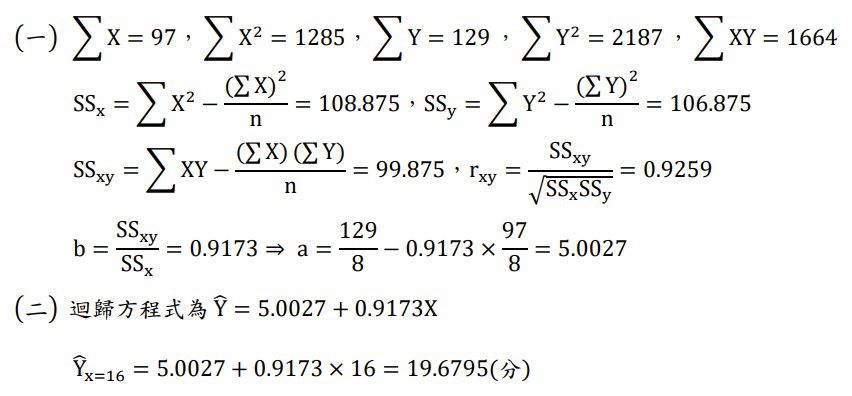
98身障三等
10 位父親與其子的身高，父親身高 ( X ) 的平均數為 168，標準差為 5；兒子身高 ( Y ) 的平均數為 172，標準差為 6，父子身高之間的共變數(C_xy)為 24，試回答下列問題：(25分)
(一)相關係數?
(二)X 對 Y 的直線方程式?
(三)若甲生父親的身高為 174 公分，預測其子身高?
(四)求 X 預測 Y 的標準迴歸係數( β_y•x )?
(五)求 X 預測 Y 的估計標準誤( σ_y•x )?

參考答案

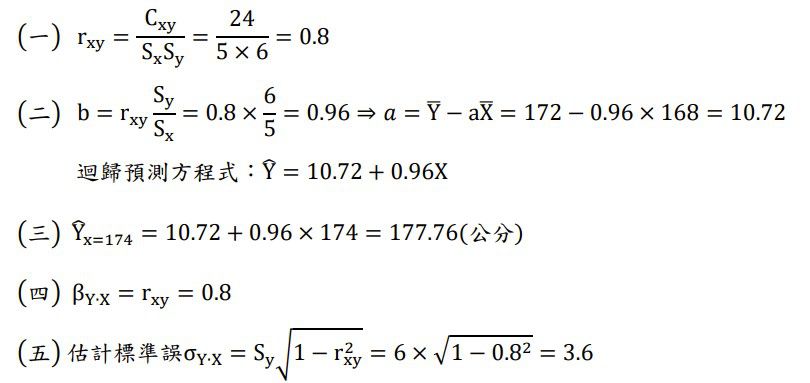
109高考
某位統計學家根據 81 名抽樣學生的努力程度( X，單位：小時 )與學業成績 ( Y，單位：分) 兩個變項分數，建立起一條迴歸方程式及其估計參數如下所示：
其中，方程式的截距項估計值 ( I 值)為 62.75，斜率項估計值( B 值 )為 0.8，其估計標準誤SE(B) 為 0.125，整條方程式的決定係數為 R²= .81。請問：
(一)經檢定結果，該迴歸係數是否已達顯著( α= .05 時，查表臨界點 t = ±2 )？
(二)努力程度 ( X ) 與學業成績 ( Y ) 個變項之間的相關係數是多少？
(三)若某考生的努力程度為 10 小時，則預測該考生的學業成績為幾分？
(四)若將上述的 X 與 Y 兩變項均標準化後，再求其迴歸方程式，則方程式該如何表達？
(五)若該統計學家想改以學業成績 ( Y )來預測努力程度 ( X )的話，則該預測結果的標準化迴歸方程式應該如何表達？

參考答案

106地特四等
一位老師以期中考成績預測期末考成績，其迴歸方程式之常數為 40，迴歸係數為 0.5，請回答下列問題：
(一)何謂簡單線性迴歸？寫出本題線性迴歸方程式。( 10 分 )
(二)若期中與期末成績之相關係數為 0.6，說明相關係數與迴歸係數之關係。( 10 分 )
(三)若題(一)的線性迴歸方程式之迴歸常數調整成為 50，而迴歸係數為 0.4 時，三位學生期中考成績分別為小祐：40 分；小如：80 分；小助：100 分，請計算其期末考之預測成績分別為何？( 5 分)

參考答案

105地特三等
某教育統計學者擬進行以「成就動機」( X 變項) 預測「學業成績」( Y 變項 )的迴歸分析研究，但因為熬夜工作，頭昏眼花，錯把初步獲得的標準化迴歸公式寫成下列的式子：
成就動機＝ 0.5 × 學業成績
請回答下列問題：
(一)他原本打算獲得的標準化迴歸公式應該表示為何？（5 分）
(二)成就動機可以預測到學業成績多少百分比的變異量？（5 分）
(三)事後他仔細一想，若改成以「學業成績」預測「成就動機」的結果才是合理的話，則該預測公式的決定係數為何？（5 分）
(四)經過這兩次的測試分析，他終於發現以「成就動機」預測「學業成績」的標準化迴歸係數，和以「學業成績」預測「成就動機」的標準化迴歸係數，彼此間有何不同？請說明之。（10 分）